跳转至

其他优化器

作者：Robert Andrew Martin

译者：片刻小哥哥

项目地址：https://portfolio.apachecn.org/OtherOptimizers

原始地址：https://pyportfolioopt.readthedocs.io/en/latest/OtherOptimizers.html

有效的前沿方法涉及受约束的目标的直接优化。然而，有一些投资组合优化方案的性质完全不同。PyPortfolioOpt 为这些替代方案提供支持，同时仍然允许您访问相同的预处理和后处理 API。

笔记

从 v0.4 开始，这些其他优化器现在继承自 BaseOptimizer 或 BaseConvexOptimizer，因此您不再需要自己实现预处理和后处理方法。 因此，您可以轻松地将 EfficientFrontier 替换为 HRPOpt。

分级风险平价 (HRP)

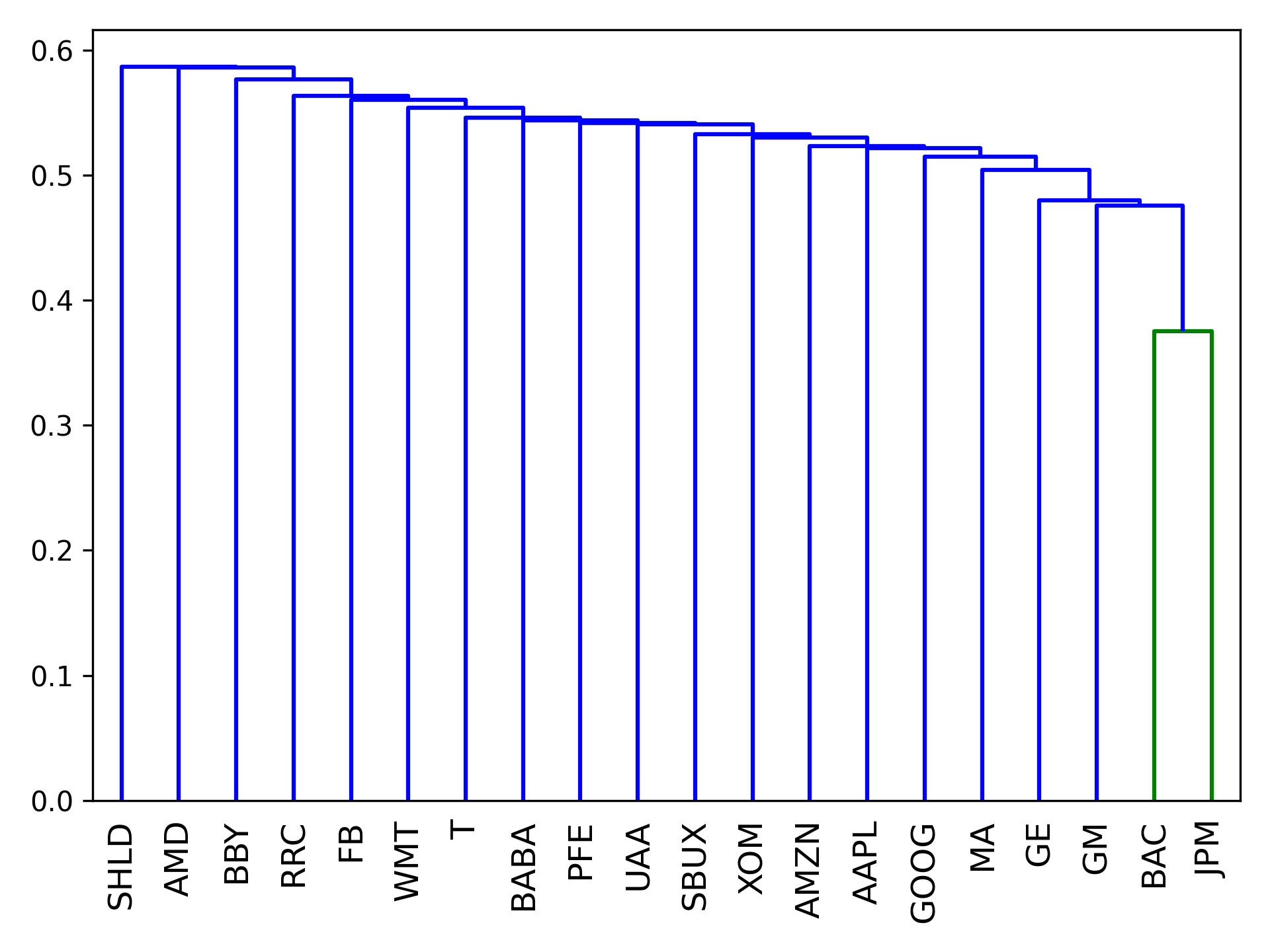
分层风险平价是 Marcos Lopez de Prado 开发的一种新颖的投资组合优化方法 [1]。 虽然可以在链接的论文中找到详细的解释，但以下是 HRP 工作原理的粗略概述：

  1. 从资产范围中，根据资产的相关性形成距离矩阵。
  2. 使用这个距离矩阵，通过层次聚类将资产聚类成树
  3. 在树的每个分支内，形成最小方差投资组合(通常仅在两个资产之间)。
  4. 迭代每个级别，在每个节点优化组合迷你投资组合。

这样做的优点是，它不需要像传统的均值-方差优化那样对协方差矩阵进行求逆，并且似乎可以产生在样本外表现良好的多样化投资组合。

聚类图

hierarchical_portfolio 模块旨在实现投资组合优化的最新进展之一 —— 分层聚类模型在分配中的应用。

所有分层类都具有与 EfficientFrontier 类似的 API，但由于许多分层模型当前不支持不同的目标，因此实际分配是通过调用 optimize() 进行的。

目前实施：

  • HRPOpt 实施分级风险平价 (HRP) 投资组合。 代码经 Marcos Lopez de Prado (2016) 许可复制。

class pypfopt.hierarchical_portfolio.HRPOpt(returns=None, cov_matrix=None) [来源]

HRPOt 对象(继承自 BaseOptimizer)构造了一个层次结构 风险平价投资组合。

实例变量：

  • 输入
    • n_assets - int
    • tickers - str list
    • returns - pd.DataFrame
  • 输出：
    • weights - np.ndarray
    • clusters - 对应于集群资产的链接矩阵。

公共方法：

  • optimize() 使用 HRP 计算权重
  • portfolio_performance() 计算预期回报、波动率和夏普比率优化的投资组合。
  • set_weights() 从权重字典创建 self.weights (np.ndarray)
  • clean_weights() 将 weights and clips 四舍五入到接近零。
  • save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(returns=None, cov_matrix=None) [来源]

Parameters:

  • return ( pd.DataFrame ) – 资产历史回报
  • cov_matrix ( pd.DataFrame ) – 资产回报的协方差

Raises: TypeError - 如果 returns 不是dataframe

optimize(linkage_method='single') [来源]

使用 Scipy 分层聚类构建分层风险平价投资组合(看 此处 )

Parameters: linkage_method ( str ) – 使用哪种 scipy 链接方法

Returns: HRP 投资组合的权重

Return type: 有序字典

portfolio_performance(verbose=False, risk_free_rate=0.02, frequency=252) [来源]

优化后，计算(并可选择打印)最佳性能 文件夹。目前计算预期回报、波动率和夏普比率 假设每天都有回报

Parameters:

  • verbose ( bool, optional ) – 是否应该打印性能，默认为 False
  • risk_free_rate ( float, optional ) – 无风险借贷利率，默认为0.02。无风险利率的期限应与预期回报的频率。
  • frequency ( int, optional ) – 一年中的时间段数，默认为 252(一年中的交易日数)

Raises: ValueError – 如果尚未计算权重

Returns: 预期回报、波动性、夏普比率。

Return type: (float、float、float)

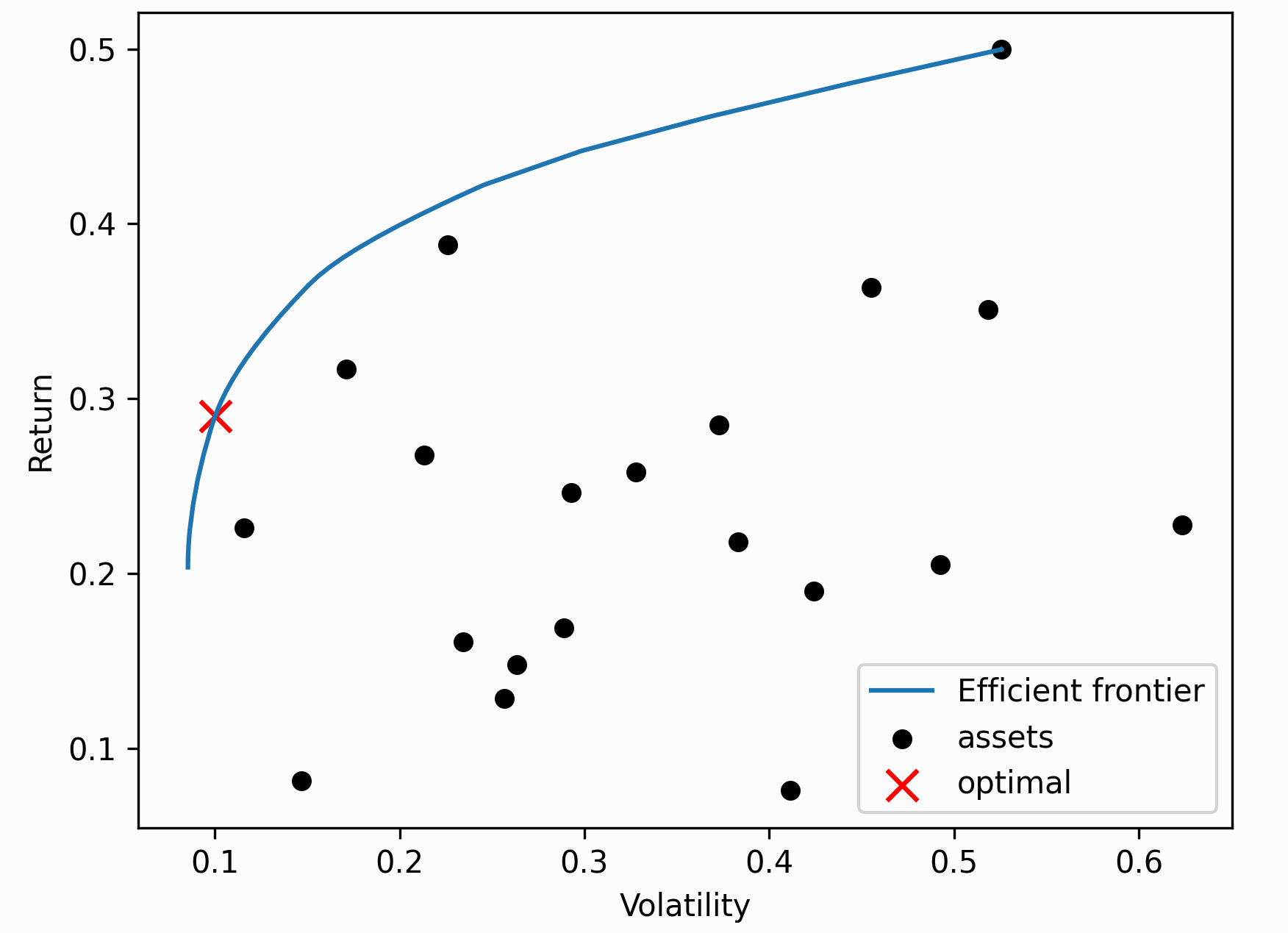
临界线算法

这是用于寻找均值方差最优投资组合的二次求解器的强大替代方案， 当我们应用线性不等式时，这尤其有利。与一般的凸优化例程不同， CLA 专为投资组合优化而设计。保证一定时间后收敛 迭代次数，并且可以有效地导出整个有效前沿。

有效前沿

提示

一般来说，除非您有特定的要求，例如您想有效地计算整个有效边界以进行绘图，否则我会使用标准的 EfficientFrontier 优化器。

我非常感谢 Marcos López de Prado 和 David Bailey 提供的实施[2]。 已通过电子邮件收到其分发许可。 它已被修改为具有相同的 API，但从 v0.5.0 开始，我们仅支持 max_sharpe() 和 min_volatility()。

cla 模块包含 CLA 类，该类使用 Marcos Lopez de Prado 和 David Bailey 实施的临界线算法生成最佳投资组合。

class pypfopt.cla.CLA(expected_returns, cov_matrix, weight_bounds=(0, 1)) [来源]

实例变量：

  • 输入：
    • n_assets - int
    • tickers - str list
    • 平均值 - np.ndarray
    • cov_matrix - np.ndarray
    • expected_returns - np.ndarray
    • 磅 - np.ndarray
    • ub - np.ndarray
  • 优化Parameters:
    • w - np.ndarray 列表
    • ls - floatlist
    • g - floatlist
    • f - floatlist
  • 输出：
    • weights - np.ndarray
    • frontier_values - (float list、float list、np.ndarray list)

公共方法：

  • max_sharp() 优化最大夏普比率(又称切线投资组合)
  • min_volatility() 优化以最小化波动性
  • efficient_frontier() 计算整个有效边界
  • portfolio_performance() 计算预期回报、波动率和夏普比率优化的投资组合。
  • clean_weights() 将 weights and clips 四舍五入到接近零。
  • save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(expected_returns, cov_matrix, weight_bounds=(0, 1)) [来源]

Parameters:

  • expected_returns ( pd.Series, list, np.ndarray ) – 每项资产的预期回报。如果设置为无仅针对波动性进行优化。
  • cov_matrix ( pd.DataFrame 或者 np.array ) – 每项资产收益的协方差
  • weight_bounds ( tuple(float, float) 或者(list/ndarray, list/ndarray) 或者list(tuple(float, float))* ) – 资产的最小和最大权重，默认为 (0, 1)。对于做空的投资组合，必须更改为 (-1, 1)。

Raises:

  • TypeError - 如果 expected_returns 不是series, list 或 array
  • TypeError - 如果 cov_matrix 不是dataframe或array

efficient_frontier(points=100) [来源]

有效计算整个有效边界

Parameters: points ( int, optional ) – 要评估的粗略点数，默认为 100

Raises: ValueError – 如果权重尚未计算

Returns: 返回 list、std list、weight list

Return type: (float list、float list、np.ndarray list)

max_sharpe() [来源]

最大化夏普比率。

Returns: 最大夏普投资组合的资产权重

Return type: 有序字典

min_volatility() [来源]

最大限度地减少波动性。

Returns: 波动性最小化投资组合的资产权重

Return type: 有序字典

portfolio_performance(verbose=False, risk_free_rate=0.02) [来源]

优化后，计算(并可选择打印)最佳性能 文件夹。目前计算预期回报、波动率和夏普比率。

Parameters:

  • verbose ( bool, optional ) – 是否应该打印性能，默认为 False
  • risk_free_rate ( float, optional ) – 无风险借贷利率，默认为0.02

Raises: ValueError – 如果尚未计算权重

Returns: 预期回报、波动性、夏普比率。

Return type: (float、float、float)

set_weights() [来源]

根据用户输入设置权重属性(np.array)的实用函数

Parameters: input_weights ( dict ) – {ticker: weight} dict

实施您自己的优化器

请注意，这与实现 自定义优化问题 有很大不同，因为在这种情况下我们仍然使用相同的凸优化结构。 然而，HRP 和 CLA 优化具有根本不同的优化方法。 一般来说，与自定义目标函数相比，这些函数的编码要困难得多。

要实现与 PyPortfolioOpt 其余部分兼容的自定义优化器，只需扩展 BaseOptimizer(如果要使用 cvxpy，则扩展 BaseOptimizer)，两者都可以在 base_optimizer.py 中找到。 这使您可以访问 clean_weights() 等实用程序方法，并确保任何输出与 portfolio_performance() 和后处理方法兼容。

base_optimizer 模块包含所有优化器都将从中继承的父类 BaseOptimizer。 BaseConvexOptimizer 是所有 cvxpy(和 scipy)优化的基类。

此外，我们定义了一个通用效用函数 portfolio_performance 来评估给定的一组投资组合权重的回报和风险。

class pypfopt.base_optimizer.BaseOptimizer(n_assets, tickers=None) [来源]

实例变量：

  • n_assets - int
  • tickers - str list
  • weights - np.ndarray

公共方法：

  • set_weights() 从权重字典创建 self.weights (np.ndarray)
  • clean_weights() 将 weights and clips 四舍五入到接近零。
  • save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(n_assets, tickers=None) [来源]

Parameters:

  • n_assets ( int ) – 资产数量
  • tickers ( list ) – 资产名称

clean_weights(cutoff=0.0001, rounding=5) [来源]

清理原始权重的辅助方法，设置其绝对值的任何权重 值低于截止值为零，并将其余部分四舍五入。

Parameters:

  • cutoff ( float, optional ) – 下限，默认为 1e-4
  • rounding ( int, optional ) – 权重四舍五入的小数位数，默认为 5。如果不需要舍入，则设置为 None。

Returns: 资产权重

Return type: 有序字典

save_weights_to_file(filename='weights.csv') [来源]

将权重保存到文本文件的实用方法。

Parameters: filename ( str ) – 文件名。应为 csv、json 或 txt。

set_weights(input_weights) [来源]

根据用户输入设置权重属性(np.array)的实用函数

Parameters: input_weights ( dict ) – {ticker: weight} dict

class pypfopt.base_optimizer.BaseConvexOptimizer(n_assets, tickers=None, weight_bounds=(0, 1), solver=None, verbose=False, solver_options=None) [来源]

BaseConvexOptimizer 包含许多供 cvxpy 使用的私有变量。 例如，权重的不可变优化变量存储为 self._w。 不鼓励直接与这些变量进行交互。

实例变量：

  • n_assets - int
  • tickers - str list
  • weights - np.ndarray
  • _opt - cp.Problem
  • _solver - STR
  • _solver_options - {str: str} dict

公共方法：

  • add_objective() 向优化问题添加(凸)目标
  • add_constraint() 为优化问题添加约束
  • convex_objective() 求解具有线性约束的通用凸目标
  • nonconvex_objective() 使用 scipy 后端求解通用非凸目标。 这很容易陷入局部最小值，通常不推荐。
  • set_weights() 从权重字典创建 self.weights (np.ndarray)
  • clean_weights() 将 weights and clips 四舍五入到接近零。
  • save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(n_assets, tickers=None, weight_bounds=(0, 1), solver=None, verbose=False, solver_options=None) [来源]

Parameters:

  • weight_bounds ( tuple 或 tuple list, optional ) – 每个资产的最小和最大权重或单个最小/最大对(如果全部相同)默认为 (0, 1)。 对于做空的投资组合，必须更改为 (-1, 1)。
  • solver ( str, optional ) – 求解器的名称。列出可用的求解器： cvxpy.installed_solvers()
  • verbose ( bool, optional ) – 是否应该打印性能和调试信息，默认为 False
  • solver_options ( dict, optional ) – 给定求解器的参数

_map_bounds_to_constraints(test_bounds) [来源]

将输入边界转换为 cvxpy 可接受的形式并添加到约束列表中。

Parameters:

test_bounds ( * tuple 或 list/tuple 的tuple 或 np arrays* ) – 每个资产的最小和最大重量或单个最小/最大对(如果全部相同)或对应于下限/上限的数组对。 默认为 (0, 1)。

Raises: TypeError - 如果 test_bounds 类型不正确

Returns: 适合 cvxpy 的边界

Return type: np.ndarray 的tuple对

_solve_cvxpy_opt_problem() [来源]

解决 cvxpy 问题并检查输出的辅助方法， 一旦目标和限制已经确定

Raises: exceptions.OptimizationError – 如果问题无法通过 cvxpy 解决

add_constraint(new_constraint) [来源]

向优化问题添加新的约束。该约束必须满足 DCP 规则， 即是线性等式约束或凸不等式约束。

例子：

ef.add_constraint(lambda x : x[0] == 0.02)
ef.add_constraint(lambda x : x >= 0.01)
ef.add_constraint(lambda x: x <= np.array([0.01, 0.08, ..., 0.5]))

Parameters: new_constraint ( 可调用(例如 lambda 函数)* ) – 要添加的约束

add_objective(new_objective, **kwargs) [来源]

在目标函数中添加一个新项。该项必须是凸的， 并由 cvxpy 原子函数构建。

例子：

def L1_norm(w, k=1):
    return k \* cp.norm(w, 1)

ef.add_objective(L1_norm, k=2)

Parameters: new_objective ( cp.Expression(即 cp.Variable 的函数)* ) – 要添加的目标

add_sector_constraints(sector_mapper, sector_lower, sector_upper) [来源]

添加对不同资产组的权重总和的约束。 最常见的是，这些将是行业限制，例如投资组合的风险敞口 tech 必须小于 x%：

sector_mapper = {
    "GOOG": "tech",
    "FB": "tech",,
    "XOM": "Oil/Gas",
    "RRC": "Oil/Gas",
    "MA": "Financials",
    "JPM": "Financials",
}

sector_lower = {"tech": 0.1}  # at least 10% to tech
sector_upper = {
    "tech": 0.4, # less than 40% tech
    "Oil/Gas": 0.1 # less than 10% oil and gas
}

Parameters:

  • sector_mapper ( {str: str} dict ) – 将股票代码映射到 sector 的字典
  • sector_lower ( {str: float} dict ) – 每个 sector 的下限
  • sector_upper ( {str: float} dict ) – 每个 sector的上限

convex_objective(custom_objective, weights_sum_to_one=True, **kwargs) [来源]

优化自定义凸目标函数。应添加约束 ef.add_constraint() 。优化器参数必须作为关键字参数传递。例子：

# Could define as a lambda function instead
def logarithmic_barrier(w, cov_matrix, k=0.1):
    # 60 Years of Portfolio Optimization, Kolm et al (2014)
    return cp.quad_form(w, cov_matrix) - k \* cp.sum(cp.log(w))

w = ef.convex_objective(logarithmic_barrier, cov_matrix=ef.cov_matrix)

Parameters:

  • custom_objective (带有签名的函数 (cp.Variable, kwargs) -> cp.Expression) – 要最小化的目标函数。 这应该使用 cvxpy 原子编写 应该映射 (w, kwargs) -> float。
  • weights_sum_to_one (bool, optional) – 是否添加默认目标，默认为 True

Raises: OptimizationError – 如果目标是非凸的或约束是非线性的。

Returns: 有效风险投资组合的资产权重

Return type: 有序字典

deepcopy() [来源]

返回优化器的自定义深层副本。这是必要的，因为 cvxpy 表达式不支持深度复制，但可变参数需要 复制以避免意外的副作用。相反，我们创建一个浅拷贝 优化器的，然后手动复制可变参数。

nonconvex_objective(custom_objective, objective_args=None, weights_sum_to_one=True, constraints=None, solver='SLSQP', initial_guess=None) [来源]

使用 scipy 后端优化一些目标函数。这个可以 支持非凸目标和非线性约束，但可能会卡住 在局部最小值。例子：

# Market-neutral efficient risk
constraints = [
    {"type": "eq", "fun": lambda w: np.sum(w)},  # weights sum to zero
    {
        "type": "eq",
        "fun": lambda w: target_risk \*\* 2 - np.dot(w.T, np.dot(ef.cov_matrix, w)),
    },  # risk = target_risk
]
ef.nonconvex_objective(
    lambda w, mu: -w.T.dot(mu),  # min negative return (i.e maximise return)
    objective_args=(ef.expected_returns,),
    weights_sum_to_one=False,
    constraints=constraints,
)

Parameters:

  • target_function ( 带签名的函数(np.ndarray, args)-> float ) – 要最小化的目标函数。这个功能 应该映射(权重，args)->成本
  • target_args ( np.ndarrays 的 tuple ) – 目标函数的参数(不包括权重)
  • weights_sum_to_one ( bool, optional ) – 是否添加默认目标，默认为True
  • constraints ( dict list ) – scipy 格式的约束列表(即字典)
  • solver ( string ) – 使用哪个 SCIPY 求解器，例如“SLSQP”、“COBYLA”、“BFGS”。 用户注意：不同的优化器需要不同的输入。
  • initial_guess ( np.ndarray ) – weights, shape (n,) 或 (n, 1) 的初始猜测

Returns: 优化自定义目标的资产权重

Return type: 有序字典

参考文献

回到顶部